Effect of breed composition in genomic prediction using crossbred pig reference population

The genotype dataset comprised data from 354 Duroc × Korean native pigs (DK), 1,105 Landrace × Korean native pigs (LK), 1,017 Landrace × Yorkshire × Duroc (LYD) crossbreds, along with purebred animals. Crossbred individuals were genotyped using the Illumina PorcineSNP60 Genotyping BeadChip, whereas genotype data for purebred animals were provided by the Centre for Research in Agricultural Genomics [12]. Genotype data for the Korean native pigs (KNPs) among the purebreds were provided by the National Institute of Animal Science in Korea. Details regarding the number of animals, single nucleotide polymorphisms (SNPs), and average observed heterozygosity rate for each breed are presented in Table 1. The quality control process involved the exclusion of SNPs located on sex chromosomes, with a genotype call rate below 90%, and with a minor allele frequency below 1%. After merging datasets and applying the quality control process, a common set of 24,118 SNPs were retained for analysis.

Phenotypic data revealed differences in backfat thickness and carcass weight among the breeds. The LYD breed exhibited the lowest backfat thickness, whereas the DK breed had the highest backfat thickness. Conversely, the DK breed exhibited the lowest carcass weight, whereas LYD had the highest carcass weight. The carcass performance of the breeds crossed with the KNP was lower than that of LYD. This finding aligns with the known characteristics of the KNP breed, which is known for its good meat quality but poor growth rate [13]. Statistical details for the phenotypes are provided in Table 2.

Principal component analysis (PCA) was employed to investigate genetic differences between populations and to correct for population structure. PCA simplifies data complexity while maintaining the underlying relationships among the data points. When applied to biallelic genotype data, PCA identifies the eigenvalues and eigenvectors of the covariance matrix of allele frequencies, thereby reducing the data to a limited number of dimensions known as PCs. Each PC represents a proportion of the total genomic variation. Subsequently, the data are mapped onto the space defined by these PC axes, facilitating the visualization of samples and their distances from each other in a scatter plot. In this visualization, sample overlap indicates shared genetic identity, reflecting common ancestry or origin [14].

Genomic breed composition (GBC) was estimated from genomic data using a maximum likelihood model implemented in ADMIXTURE v1.3.0 [15]. ADMIXTURE uses genotype data to cluster individuals into subgroups based on a predetermined number of groups. The projection extension of the ADMIXTURE program allows for estimating ancestry using predefined ancestral population allele frequencies. This extension enables efficient ancestry inference across large genomic datasets, leveraging allele frequencies from reference panels, such as the 1000 Genomes Project. Additionally, the projection approach is particularly advantageous for datasets with significant population distribution imbalances, as such imbalances can adversely affect the accuracy of ancestry inference [16].

The projection extension of the ADMIXTURE program was used to analyze the dataset owing to the imbalance between purebred and crossbred samples. Ancestral population allele frequencies were estimated using the purebred samples, whereas the GBC values of the crossbreds were estimated using the allele frequencies of the purebreds.

First, PCs and GBCs were calculated for each individual, which were subsequently used in five models to predict genomic estimated breeding values (GEBV). Although additional fixed effects such as age and farm were considered, age information was unavailable, and farm data showed high multicollinearity with the PC and GBC values, which precluded their inclusion.

Model 1 (NULL) is defined as follows:

where y represents the vector of trait records (backfat thickness or carcass weight); b indicates the vector of fixed effects, including sex; X denotes the design matrix linking fixed effects to the records; g represents the vector of random genetic effects, modeled as $\sim N\left(0,G{\sigma }_g^2\right)$, with G being the genomic relationship matrix and ${\sigma }_g^2$ being the genetic variance captured by the SNPs; Z indicates the design matrix linking records to animals; and e denotes the vector of random deviations, modeled as $\sim N\left(0,I{\sigma }_g^2\right)$, with I as an animal-by-animal identity matrix and ${\sigma }_e^2$ representing the error variance. The GEBV for this model was predicted as GEBV = ĝ. The genomic relationship matrix was constructed using GCTA v1.94.1 software according to the following equation [17]:

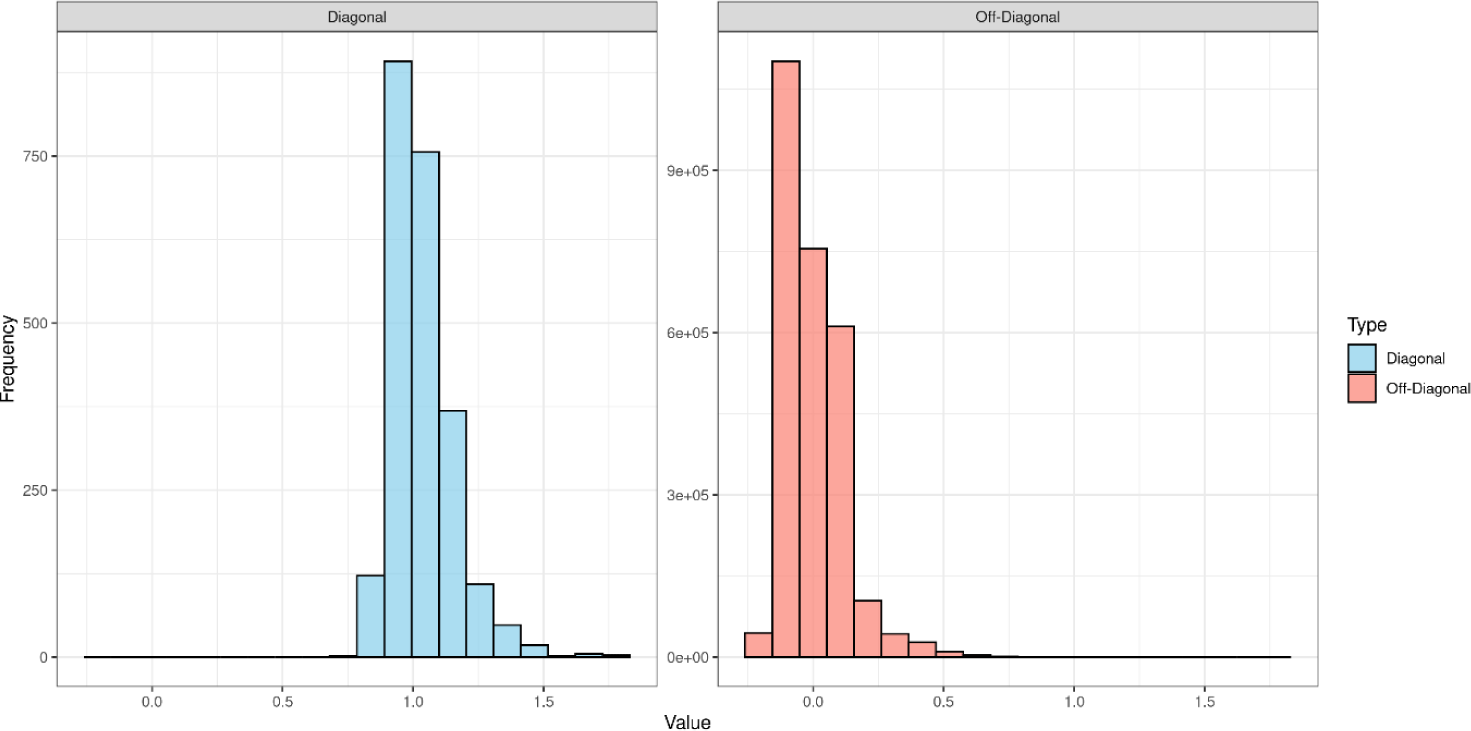
where x_ij and x_ik represent the genotypes (coded as 0, 1, or 2) of individuals j and k at SNP i. p_i indicates the allele frequency of SNP i, and N denotes the total number of SNPs. The distribution of the diagonal and off-diagonal elements of the genomic relationship matrix is shown in Fig. 1. The mean of the diagonal elements is 1.03, indicating low inbreeding within the population. The mean of the off-diagonal elements is 0, showing that individuals are genetically independent of each other.

Fig. 1. Distribution of diagonal and off-diagonal elements of the genomic relationship matrix.

Download Original Figure

Model 2 (PC_F) is defined as follows:

where y represents the vector of trait records; b denotes the vector of fixed effects, which includes PC values (20 PCs) and sex; X indicates the design matrix linking fixed effects to records; g represents the vector of random genetic effects; Z denotes the design matrix linking records to animals; and e indicates the vector of random deviations. For this model, GEBV = ĝ.

Model 3 (GBC_F) is defined as follows:

where y represents the vector of trait records; b denotes the vector of fixed effects, which includes GBC values and sex (here, breed composition values represent the proportion of each individual’s genome derived from the four breeds: Duroc, KNP, Landrace, and Yorkshire); X indicates the design matrix linking fixed effects to records; g represents the vector of random genetic effects; Z denotes the design matrix linking records to animals; and e indicates the vector of random deviations. For this model, GEBV = ĝ.

Model 4 (PC_R) is defined as follows:

where y indicates the vector of trait records; b represents the vector of fixed effects, including sex; X denotes the design matrix linking fixed effects to records; g indicates the vector of random genetic effects; pc denotes the vector of random variables representing groups of PC values, which were clustered using the Gaussian Mixture Model implemented in the ‘mclust’ R package [18]; Z indicates the design matrix linking records to animals; and e denotes the vector of random deviations. For this model, $\text{GEBV}=\widehat{g}+\widehat{\text{pc}}$.

Model 5 (GBC_R) is defined as follows:

where y represents the vector of trait records; b denotes the vector of fixed effects, including sex; X indicates the design matrix linking fixed effects to records; g represents the vector of random genetic effects; gbc denotes the vector of random variables representing groups of GBC values, which were clustered using the Gaussian Mixture Model implemented in the ‘mclust’ R package [18]; Z indicates the design matrix linking records to animals; and e represents the vector of random deviations. For this model, $\text{GEBV}=\widehat{g}+\widehat{\text{gbc}}$.

Variance components were estimated using the restricted maximum likelihood (REML) method, as implemented in MTG2 [19], for each model. Heritability for the traits was estimated using the formula $h^2=\widehat{{\sigma }_g^2}/\left(\widehat{{\sigma }_g^2}+\widehat{{\sigma }_e^2}\right)$. The accuracy of GEBVs for each of the five models was calculated as r(GEBV,y), where y represents the phenotypes corrected for fixed effects [20]. A 5-fold cross-validation approach was used to validate the models. In this method, animals were randomly divided into five groups, with each group treated as the validation set while the remaining groups constituted the reference set.

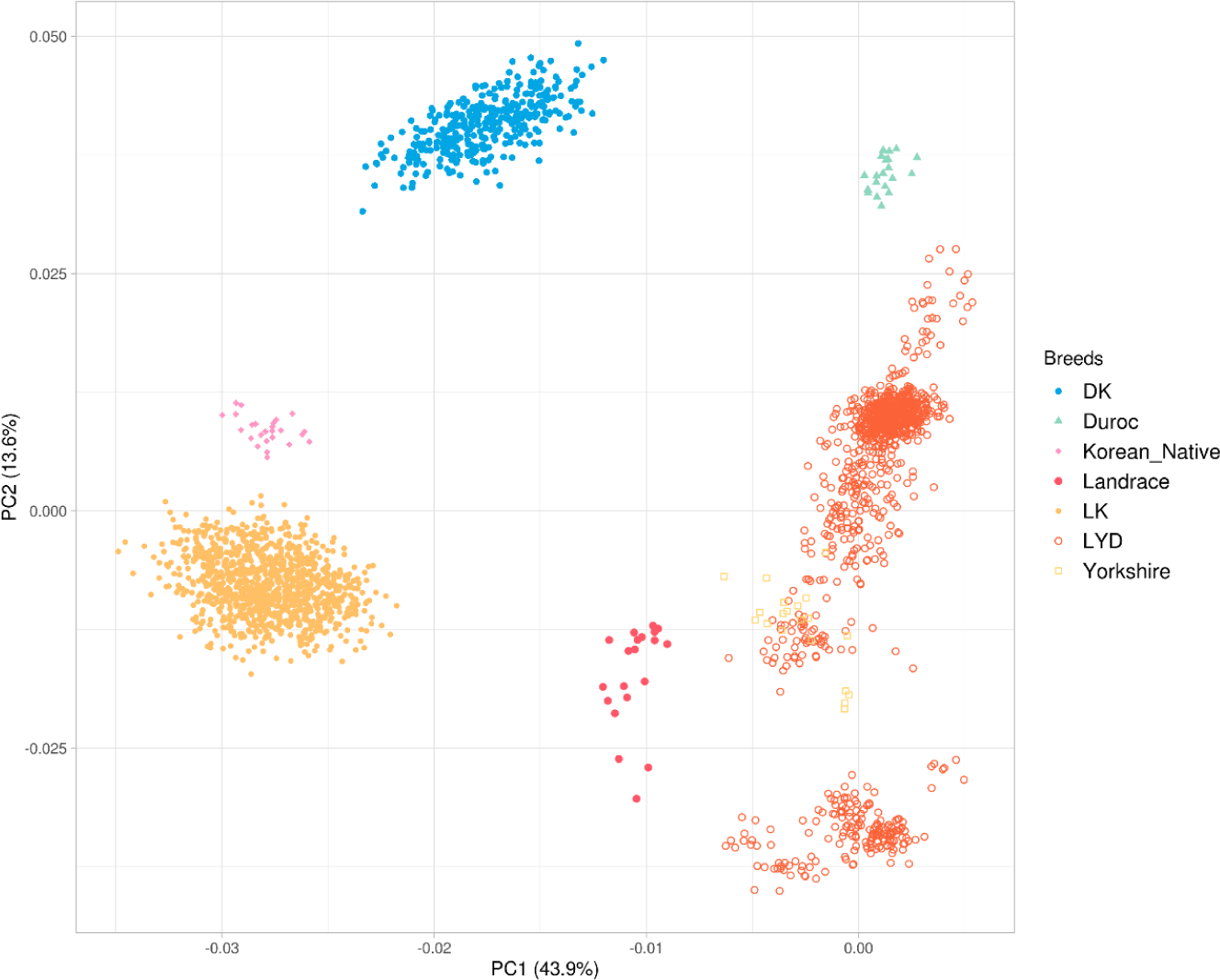
PCA was performed to explore genetic structure across populations. The analysis revealed that the first PC (PC1) accounted for 43.9% of the total genetic variance, whereas the second PC (PC2) constituted 13.6% of the variance (Fig. 2). The PCA plot revealed a clear separation among the crossbred populations, indicating distinct genetic backgrounds. However, the LYD population exhibited greater dispersion along the first two PCs, suggesting more considerable genetic variation within this group. This observed variation is likely attributed to the presence of F1 hybrids in the dataset, which primarily combined Landrace and Yorkshire genetics, thereby increasing the overall diversity observed in this population.

Fig. 2. Population distribution across the first and second principal components. PC, principal components; DK, Duroc × Korean native pigs; LK, Landrace × Korean native pigs; LYD, Landrace × Yorkshire × Duroc.

Download Original Figure

The breed composition of the crossbred populations was evaluated using ADMIXTURE analysis; the results are depicted in Fig. 3. The analysis was conducted in unsupervised mode using genomic data from purebred samples, and the estimated breed allele frequencies were subsequently used to infer breed membership coefficients for the crossbred individuals.

Fig. 3. Bar plot of the Q matrix from an ADMIXTURE run, showing the proportion of the genome contributed by each breed. (A) LYD population, (B) DK population, and (C) LK population. Each vertical bar represents an individual. KNP, Korean native pig; DK, Duroc × Korean native pig; LYD, Landrace × Yorkshire × Duroc.

Download Original Figure

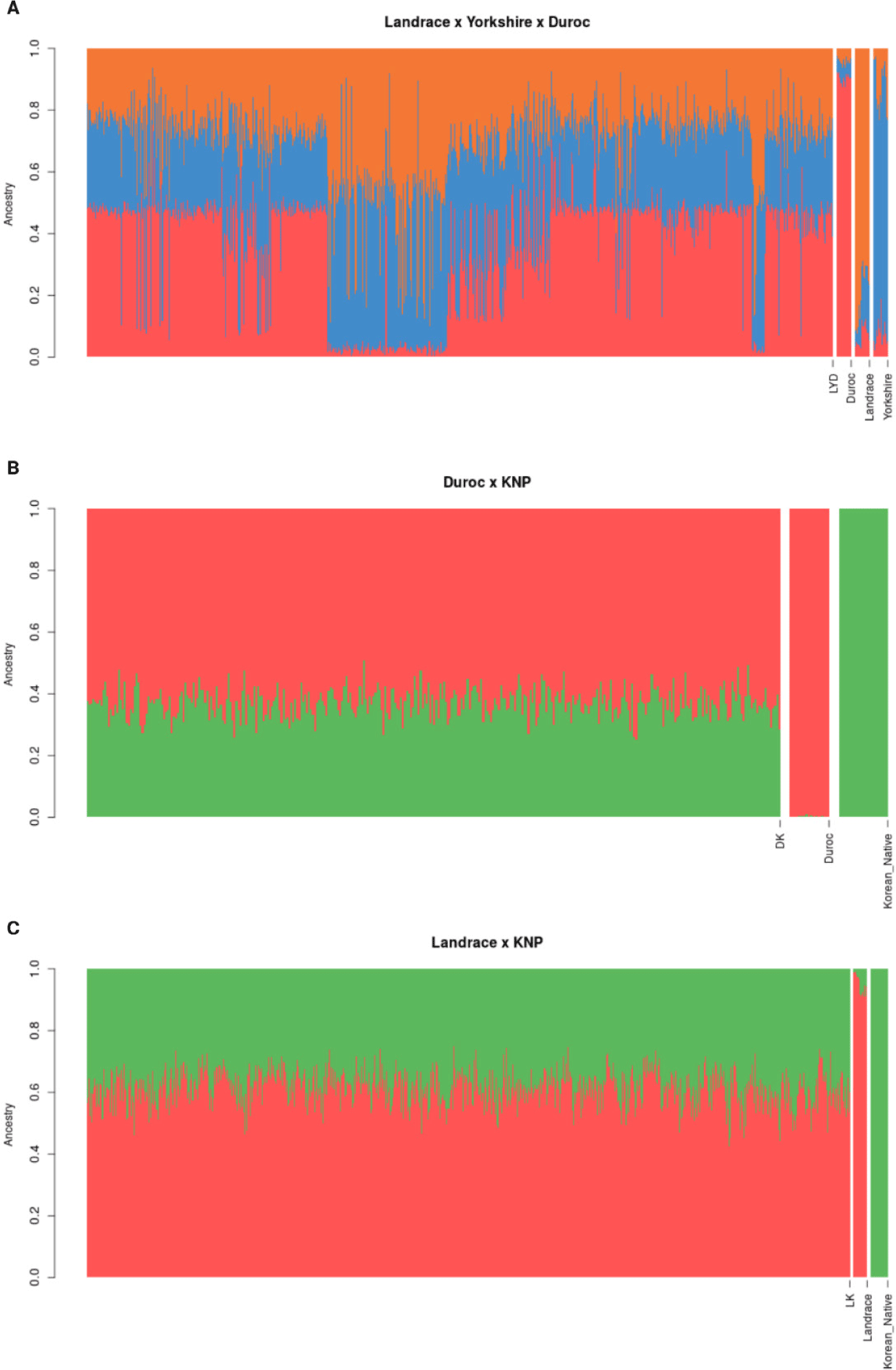
In the LYD population, the estimated breed composition revealed an average contribution of 31%, 33%, and 36% from Landrace, Yorkshire, and Duroc, respectively (Table 3). The presence of F1 animals, as indicated by the PCA, was corroborated by the breed composition analysis, where the contribution of the Landrace and Yorkshire breeds showed that the F1 crossbreds were indeed hybrids of these two pure breeds. The variation in breed composition within the LYD population was not substantial, with standard deviations of 0.13, 0.12, and 0.19 for Landrace, Yorkshire, and Duroc, respectively. Similarly, the DK and LK populations exhibited balanced breed compositions. In the DK population, the average breed composition was 63% Duroc and 37% KNP, with minimal variation between individuals (SD = 0.05 for both breeds). The LK population had an average composition of 61% Landrace and 39% KNP, and low variation was also observed across individuals (SD = 0.06 for both breeds). These results suggest that the parental breeds had relatively balanced genetic contributions, as evidenced by the minimal variation in breed composition between individuals within the DK and LK populations.

Heritability estimates for backfat thickness and carcass weight were derived from five different models; the associated variance components are detailed in Table 4. The estimates of genetic additive variance (V_g) and error variance (V_e) were used to calculate heritability for each trait.

Model 1 (NULL), which did not account for population structure, yielded the highest heritability estimates, with a heritability value of 0.44 ± 0.03 for backfat thickness and 0.31 ± 0.03 for carcass weight. The elevated heritability estimates for this model may be attributed to its lack of adjustments for potential confounding factors related to breed differences. Models 2 (PCA_F) and 3 (GBC_F), which incorporated population structure as a fixed effect, yielded lower heritability estimates; Model 2 estimated heritability for backfat thickness at 0.41 ± 0.03 and carcass weight at 0.26 ± 0.03, whereas Model 3 estimated these factors at 0.44 ± 0.03 and 0.27 ± 0.03, respectively. These reductions in heritability suggest that accounting for population structure as a fixed effect can decrease the perceived genetic influence on the traits. Models 4 (PCA_R) and 5 (GBC_R) included additional genetic variance components (V_pc and V_gbc) to account for population structure as a random effect. In Model 4, the genetic variance (V_g) was estimated at 13.2 ± 1.3 and V_pc at 1.6 ± 1.7 for backfat thickness, contributing an additional heritability of 0.05 ± 0.05 to the base estimate of 0.41 ± 0.04. For carcass weight, V_g was estimated at 28.1 ± 3.6 andV_pc at 23.7 ± 15.1, contributing an additional heritability of 0.19 ± 0.1 to the base estimate of 0.23 ± 0.04. Model 5 demonstrated similar patterns, although V_gbc for backfat thickness was close to zero. These models typically yielded heritability estimates similar to those of Model 1 for backfat thickness; however, for carcass weight, they provided a more nuanced understanding of genetic effects by accounting for population structure as a separate effect.

The accuracy of GEBVs was evaluated using five models; the results are summarized in Table 5 and depicted in Fig. 4. Model 1 (NULL), Model 4 (PCA_R), and Model 5 (GBC_R) exhibited the highest accuracy for predicting both backfat thickness and carcass weight. These models achieved an average accuracy of 0.59 for backfat thickness and 0.50 for carcass weight, with minimal variation across replicates (SD = 0.01 for backfat thickness and between 0.03 to 0.04 for carcass weight).

Fig. 4. GEBV accuracy of five prediction models. From left to right, the models are Model 1 (NULL), Model 2 (PCA_F), Model 3 (GBC_F), Model 4 (PCA_R), and Model 5 (GBC_R). The dots represent the average accuracy, and the lines indicate the standard deviation. GEBV, genomic estimated breeding value; PCA, principal component analysis; GBC, genomic breed composition.

Download Original Figure

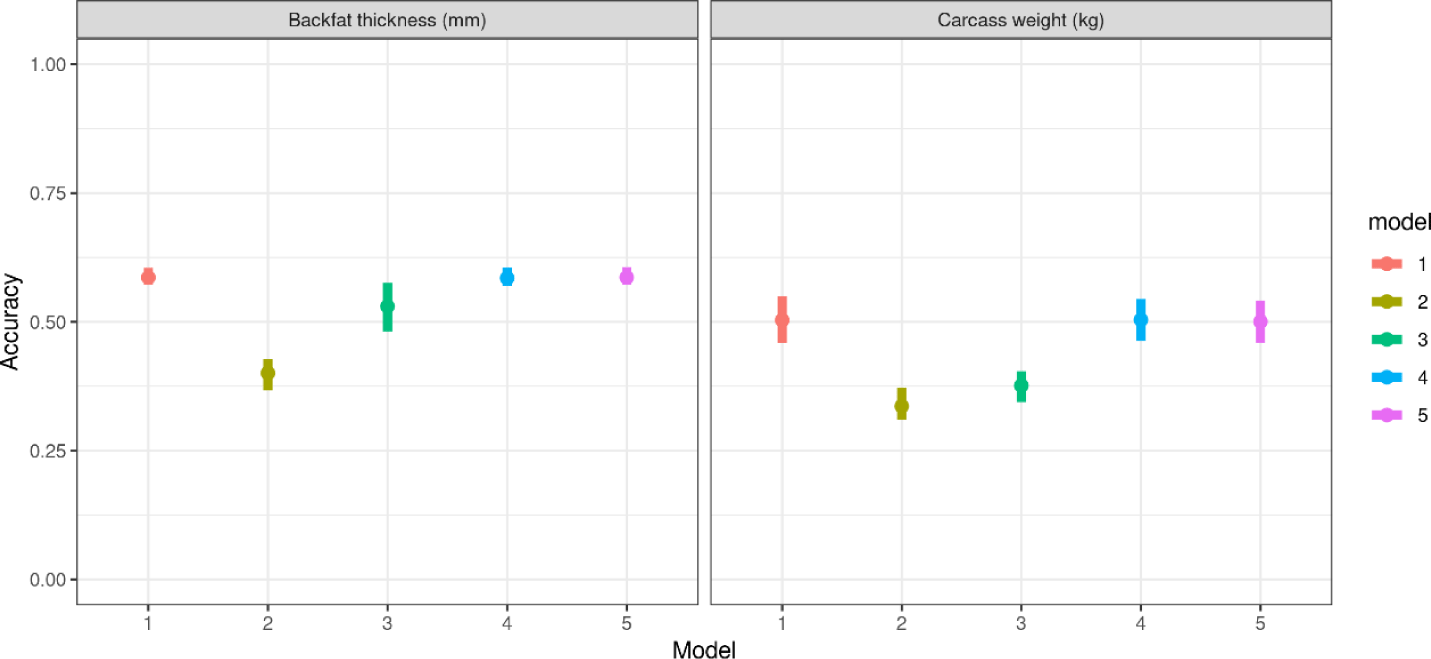
Models that incorporated population structure as a fixed effect (Models 2 and 3) demonstrated lower accuracies for GEBVs. For backfat thickness, Model 2 (PCA_F) achieved a mean accuracy of 0.40 ± 0.03, whereas Model 3 (GBC_F) yielded a mean accuracy of 0.53 ± 0.04. The accuracy for carcass weight in these models was reduced similarly, with Model 2 achieving an accuracy of 0.34 ± 0.03 and Model 3 yielding an accuracy of 0.38 ± 0.02. These results suggest that modeling population structure as a fixed effect captures population differences but compromises GEBV accuracy. In contrast, modeling population structure as a random effect captures genetic variation due to breed differences without adversely affecting GEBV accuracy.

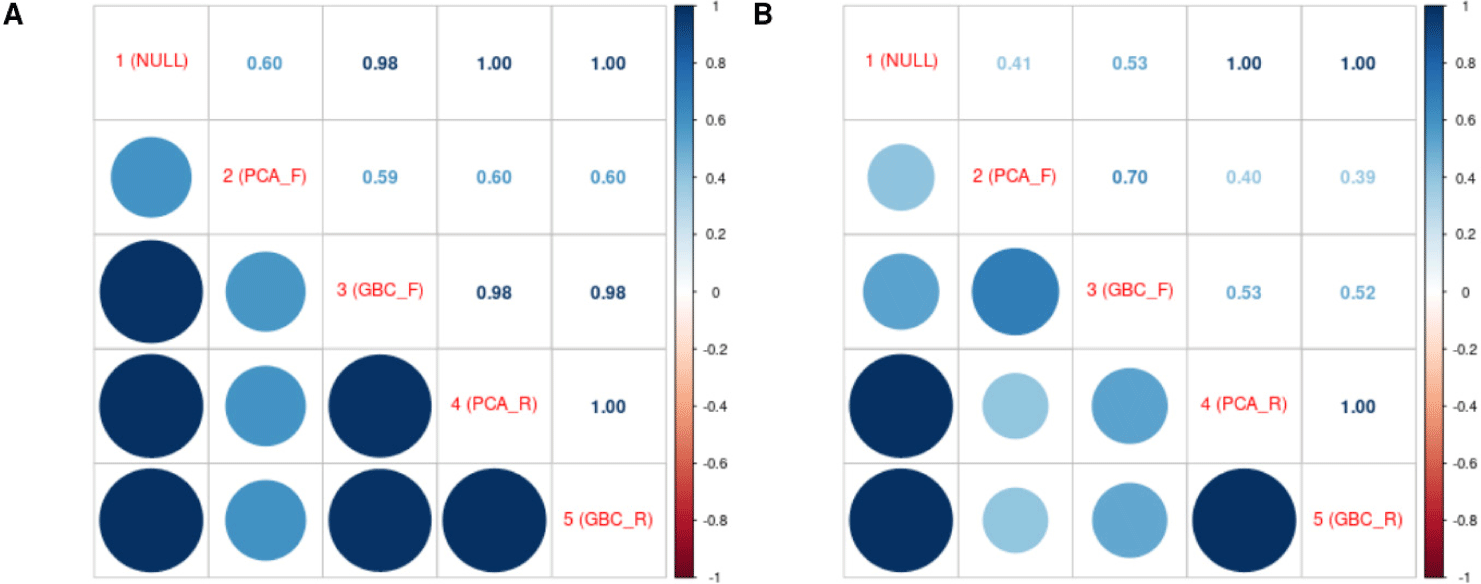
The Spearman rank correlation coefficient of GEBV between all models showed that all models were highly correlated with each other (except Model 2 in backfat thickness), ranging from 0.59 to 0.60. In carcass weight, Models 1, 4, and 5 had high Spearman correlation coefficients with each other, but models 2 and 3 had low correlation coefficients with the other models, ranging from 0.39 to 0.70 (Fig. 5). Models that did not correct for population structure and models that corrected for population structure as a random effect had similar genomic prediction patterns.

Fig. 5. Spearman correlation between models. (A) Backfat thickness and (B)carcass weight. GBC, genomic breed composition; PCA, principal componant analysis; GBC, genomic breed composition.

Download Original Figure

GBC highlights the superior accuracy of genotypic data over that of pedigree information in determining breed composition. Pedigree records often contain inaccuracies or are incomplete, which can result in erroneous breed composition estimates [21,22]. In contrast, using genomic data with tools such as ADMIXTURE provides a more precise assessment [23]. The findings of this study revealed that the breed compositions calculated using ADMIXTURE closely aligned with those expected from complete pedigree records, thereby corroborating previous research that emphasizes the reliability of genomic data for estimating breed composition in admixed populations [23].

The effect of population structure on the estimation of genetic parameters is a well-established concern in genomic studies. Population structure can lead to false-positive associations [24], which may result in inflated heritability estimates [10] and biased accuracies in genomic predictions [6]. To address this issue, this study incorporated PCs and GBCs into GBLUP models as fixed or random effects.

Notably, the inclusion of PCs or GBCs as fixed effects resulted in decreased accuracy of GEBVs compared to those of models that excluded these factors. This reduction in accuracy may stem from the redundancy between the information provided by these variables and that captured by the genomic relationship matrix. Essentially, the genomic relationship matrix already encompasses much of the population structure information; therefore, adding PCs or breed composition as fixed effects could result in double-counting, leading to overcorrection and reduced model accuracy [11,25]. In contrast, treating PCs and GBC as random effects did not yield any improvement in prediction accuracy. This result suggests that the additional genetic variance components captured by these random effects did not provide significant new information beyond what was already accounted for by the genomic relationship matrix. Similarly, previous studies have demonstrated that incorporating population structure as a random effect does not enhance the accuracy of genomic predictions [25]. However, the advantage of including breed as a random effect within the model, as GEBVs are divided into two components. Specifically, a model with a random effect splits the genetic variance into within-breed and across-breed GEBVs, thereby facilitating the understanding of how predictions differ within and across breeds [25].

These findings hold significant implications for the optimal design of genomic prediction models. Although accounting for population structure is crucial to avoid biases, these results indicate that the genomic relationship matrix within the GBLUP framework sufficiently captures the required information. Consequently, additional adjustments for population structure, whether as fixed or random effects, may be unnecessary and could even negatively affect prediction accuracy. These findings support the growing consensus that simpler models that rely on the genomic relationship matrix without further correction for population structure are often the most effective [25].

This study focused on carcass traits and therefore did not explicitly include heterozygosity, even though crossbred animals were used. However, recent findings suggest that including heterozygosity in genomic predictions for maternal traits can improve prediction accuracy [26]. Therefore, future research on maternal traits in genomic prediction models may benefit from considering heterozygosity as a factor to further enhance prediction accuracy.

Our findings have significant implications in the field of multi-breed genomic prediction. This study demonstrated that the genomic relationship matrix alone could effectively capture breed differences within multi-breed populations, thereby eliminating the necessity for additional corrections for population structure. This circumvention is particularly advantageous in multi-breed contexts, where genetic relationships among breeds can vary widely, facilitating accurate predictions of breeding values for selection decisions.

Given the observed decrease in accuracy when population structure was included as a fixed effect, future studies and practical applications of genomic prediction should prioritize models that incorporate the genomic relationship matrix as the primary tool for capturing genetic variance. This approach is more straightforward and ensures higher accuracy in predicting breeding values, which is crucial for effectively managing and improving crossbred populations.

In conclusion, this study underscores the robustness of the genomic relationship matrix in accounting for population structure within multi-breed genomic prediction. The findings suggest that, although population structure is an important consideration, the genomic relationship matrix is sufficient for capturing the relevant genetic variance, modeling additional corrections unnecessary. This insight is valuable for optimizing genomic prediction models in crossbred populations and enhancing the accuracy of GEBV predictions.