INTRODUCTION
Hanwoo is one of the oldest autochthonous cattle breeds in the world. Up to the 1960s, it was used primarily for farming on the Korean peninsula [1]. The Hanwoo has steadily been converted by Korean farmers from agricultural animals to beef cattle since the 1960s. The meat of choice in recent years has been locally raised Korean cattle, and it is priced accordingly. Hanwoo beef is renowned for its thick marbling, flavorful beefiness, and somewhat sweet flavor. It is also healthier than meat from other cattle breeds because it contains more omega-3 fatty acids with less cholesterol [2].
Reproduction traits play a vital role in the beef cattle industry as they directly influence the efficiency and profitability of production systems. Key reproductive traits, such as calving interval (CI), age at first calving (AFC), gestation length (GL), and number of artificial inseminations per conception (NAIPC), are of great importance in beef cattle breeding programs. These traits not only affect the reproductive performance of individual animals but also have significant impacts on overall herd productivity and management. A shorter calving interval enables more frequent calf production, leading to increased productivity and potential economic gains. It also facilitates efficient management practices such as grouping calves for marketing and optimizing nutrition management. AFC influences lifetime productivity and profitability, as early maturing females have an extended reproductive lifespan, resulting in a higher cumulative number of calves produced. Achieving optimal a AFC maximizes heifer utilization and minimizes costs associated with delayed breeding. GL, influencing reproductive efficiency and overall management, demands accurate knowledge for optimal calving planning, timely calving assistance, postpartum care. Furthermore, comprehending the genetic control of GL informs breeding strategies to achieve desired calving seasons and synchronization protocols. The NAIPC is crucial for reproductive success, with higher conception rates and fewer inseminations reducing costs while expediting genetic progress through more efficient use of superior sires. Improving fertility and reducing artificial inseminations enhance reproductive performance and drive increased profitability in beef cattle operations [3]. Challenges such as low reproductive capacity and infertility can result in extended durations between calvings, requiring additional interventions such as extra inseminations, increased veterinary attention, and hormonal treatments [4]. These interventions can disrupt current and subsequent lactations, leading to decreased productivity.
In cow breeding systems, the breed, sex, class, and location affect reproduction differently [5]. The outstanding performance of male and female reproduction is a requirement for effective beef production techniques. Successfully incorporating reproductive features into genetic improvement projects requires advances in analysis techniques and whole-herd reporting [5]. The estimated breeding value (EBV) and the reliability of anticipated breeding values (EBVs) are critical for selecting superior offspring to replace the present generation. The reliability of EBVs can be influenced by several factors, including selection intensity, pedigree errors, and generation interval [6]. According to the most recent studies, reproduction should be prioritized in a traditional cow-calf operation to maximize profitability. Even in a fully integrated cattle farm, reproduction necessitates an equal emphasis on attributes related to consumption and output. Genomic selection can give a large boost to the existing rates of genetic gain for beef by enhancing the accuracy of reproductive traits. The problem for cattle breeding is to improve the genetic variations identified by genomic estimations for those aspects of high genetic value that have less precision at the time of selection. The accuracy of genomic selection is currently poorer in beef cattle than in dairy cattle because of the relatively limited sample size with phenotypes and genotypes used to refine genomic prediction equations. For common heritable features, such as female reproductive traits, additional genotyped and phenotyped animals are needed to improve the accuracy of genomic predictions in beef cattle.
The Korean beef sector is seeing increased demand for genetically improving carcass qualities. The key qualities in the Hanwoo breeding program that were chosen and included in a selection index to boost the profitability of the meat industry were the carcass weight (CWT), back fat thickness (BF), eye muscle area (EMA), and marbling score (MS).
The genetic architecture of economically significant traits has been investigated regularly across many cattle populations since genotyping tools and enhanced genetic evaluation methodology emerged. Genome-wide association analyses have recently been used to find single nucleotide polymorphisms (SNPs) associated with reproduction traits in cows [7].
The correlations generally indicate how closely two traits are related [8]. A deeper knowledge of the common biological pathways and the causation linkages between two traits may be achieved by the genetic correlation, which explains the genetic relationship between two traits [9]. A strong correlation between two variables indicates their strong relationships and vice versa [10]. Typically, the correlation of the breeding values of traits is used to define the genetic correlation [11]. The genes contributing to the traits are typically co-inherited when two traits are significantly genetically connected. The phenotypic and genetic correlations are powerful tools for predicting how one trait would respond to selection due to selection on another [8]. When selecting for overall merit incorporating multiple traits, the genetic correlation reflects the degree to which two traits are affected by the same genes or genes present within the same chromosome. According to calculations of the genetic correlation between two traits, selection for one trait may indirectly affect the genetic response for the other trait [12]. The pleiotropy of genes is the leading cause of the correlation, but linkage disequilibrium can also play a role [11]. A thorough understanding of the genetic variation of economically significant reproduction and production traits and precise estimation of genetic and phenotypic correlations of economically significant traits are also necessary for establishing effective genetic improvement programs [13]. Nevertheless, the genetic and phenotypic relationships between the reproductive and carcass traits of Korean Hanwoo cattle are poorly understood. The genetic parameters, genomic prediction accuracy, and correlations (phenotypic and genetic) among reproductive and carcass traits in Hanwoo cows were calculated to achieve these goals.
MATERIALS AND METHODS
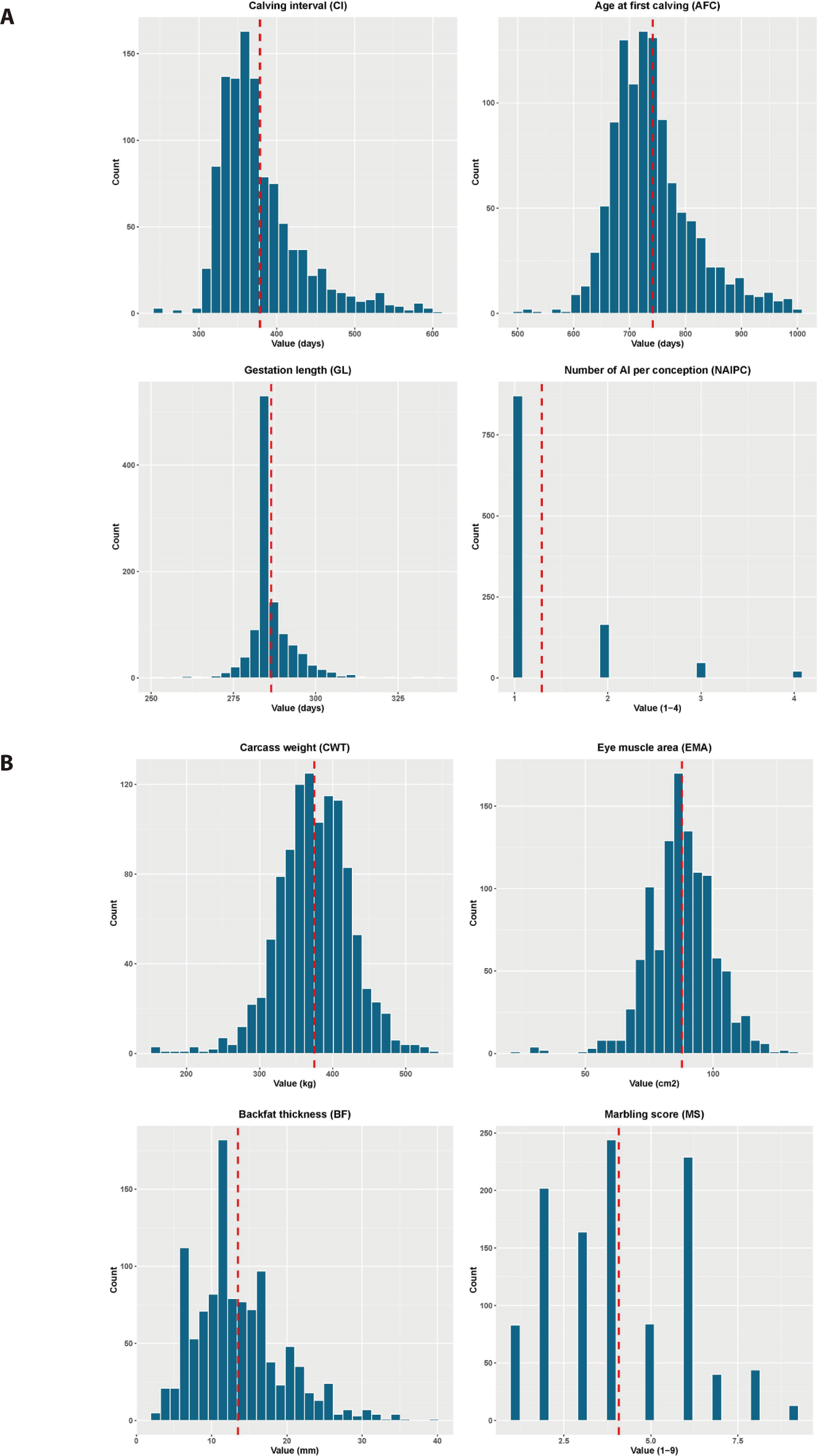
The data were collected using an existing database from 1,544 Hanwoo cows born between 2007 and 2020 and slaughtered between 2018 and 2022 and were part of nine (9) local livestock farms spread over the Gyeongsangbuk-do region in South Korea. All cows were slaughtered between 24 and 178 months of age. The analysis included reproductive traits, such as CI, AFC, GL, and the NAIPC, as well as the carcass traits like CWT, EMA, BF, and MS. The Animal Care and Use Committee’s permission was not required for this study because all the data were obtained from the existing database. After a quality assessment, the remaining data included the values for CI ranging from 242 to 601 days, AFC between 499 and 999 days, GL between 252 and 337 days, CWT between 160 and 541 kg, EMA between 22 and 131 cm2, BF between 2 and 39 mm, and MS scores between 1 and 9. The records of animals with a NAIPC above four were eliminated from the dataset. The Korean carcass grading procedure by the National Livestock Cooperatives Federation was used to record the phenotypic data for carcass traits, including CWT, EMA, BF, and MS. The CWT was measured on samples taken after 24 hours postmortem at the end of refrigeration. EMA was measured using a dot-grid method with a cross-sectional slice between the 13th rib and the 1st lumbar vertebrae perpendicular to the vertebral column, where BF was also measured. A visual assessment of the MS was conducted using a categorical system of nine levels, based on the Korean Livestock Products Grading Guideline, ranging from 1 (no marbling) to 9 (high marbling). The details of phenotypic distribution information for the studied animals are presented in Fig. 1.
The 1,544 Hanwoo cows used in this study were genotyped using Illumina Bovine 50K SNP Chip (Illumina, San Diego, CA, USA), in which 52,116 SNPs were embedded. The blood samples collected by veterinarians were used to obtain the DNA. SNPs located on sex chromosomes and with unknown and duplicate positions were removed for further quality control (QC) procedures. Several QC thresholds were set to remove poor-quality SNPs for further analysis. SNPs were discarded from the analysis when the SNP call rate was less than 90%, individuals with a genotyping call rate less than 90%, and minor allele frequency (MAF) was less than 1% (monomorphic). The genotype frequency significantly deviated (p < 0.000001) from Hardy–Weinberg Equilibrium (HWE). The identity-by-state (IBS) test was performed to determine if there were similar individuals or genotyping errors in the datasets. The pair of individuals showing a similarity rate > 99% indicates an identical animal or error in genotyping. The entire QC process and IBS test were performed through PLINK v1.9 [14]. Furthermore, the missing alleles were imputed using Beagle v5.4 software [15]. After IBS and QC, 1,526 animals with genotypes of 41,445 SNPs were available for further analysis.
The dataset fit for an animal model with a genomic relationship matrix (GRM) was performed to obtain the breeding values, including 1,103 complete records of all eight traits. The birth year and birth season were combined into one composite fixed effect. The fixed covariate of age at slaughter was also fitted with traits. The additive genetic effect of the animal was fitted as a random genetic component in the model. The genomic estimated breeding values (GEBV) were predicted using MTG2 v2.2 computer program [16]. The multi-trait animal model was implemented as follows [17]:
where y represents the vector of phenotypic records (trait) for an n-animal sample; Xb is the fixed effects [18]; Zu is the overall marker loci which are assumed to equal the vector of breeding values (a); e is the vector of random residual effect which is assumed to be normally distributed with N (0, ). In addition, where is the genetic variance, and G denotes the GRM, which was constructed using the following equation [17]:
where the marker matrix M has dimensions of n × m; n is the number of individuals; m is the number of markers used. The element of the P matrix was calculated using the formula, Pi = 2 (Pi – 0.5), where Pi represents the MAF of the marker at locus i. (M−P) represents the incidence matrix (Z) for markers.
The GRM was constructed using the genome-wide complex trait analysis (GCTA) tools developed by Yang et al. [19], which effectively retains the genomic relationship between animals [17].
The WGBLUP model and inferences were the same as the above-described GBLUP technique, which had a different way of constructing the matrix G. The G-matrix above was developed assuming that each SNP explains the same proportion of genetic variance [20]. Wang et al. [21] introduced the WGBLUP method and used the weighted G (G*) for significant SNPs with comparatively substantial effects. This GRM G* was constructed as follows [17]:
where Z, pi, and n are the same as GBLUP, and D is the diagonal matrix in the WGBLUP technique, and its values were determined by the weights derived from the SNP solutions discussed by Wang et al. [21]. Following Strandén and Garrick [22], the following can be derived:
where û is the vector of estimated SNP effects, and ĝ is a vector of GEBV from only genotyped individuals. The weight for SNP i in this study was calculated as . Constructing an algorithm for predicting D from GBLUP is possible using the above equation. The algorithm was as follows for the iterative steps of the WGBLUP, as stated by Wang et al. [21]:
-
Set t = 0, D(t) = I, where t is the iteration number, and I denotes the identity matrix.
-
The construct matrix Gt = ZD(t)Zλ, where t is the iteration number; The incidence matrix Z equals the matrix M minus matrix P, in which M is n x m where n is the number of individuals and m is the number of markers used, and P represents to 2pi.
-
Compute genomic EBV (GEBV, ĝ) utilizing the GBLUP method.
-
Calculate SNP weight as , where i is the ith SNP [23].
-
Construct the matrix G(t+1) = ZD(t+1)Z’λ.
-
t = t+1.
-
Exit or loop to steps iii or iv.
Breeding values were predicted using BLUPF90+ software [24], while the calculation of SNP effects for WGBLUP was performed using the postGSf90 software [25].
The total phenotypic variance () was calculated as follows:
The heritability (h2) values for each trait were calculated using the following formula:
where is the genetic variance; is the residual variance; and is the phenotypic variance.
The GEBV of an animal i was calculated after estimating the marker effects using the following formula below:
where m is the number of markers; is the individual i genotype at marker loci ĝj; is the allele substitution effect at locus marker j.
The following formula was used to estimate the GEBV accuracy for an animal i [26]:
where is the additive genetic variance of each trait, and PEV is the predicted error variance of the GEBV for each animal. The inverse of the coefficient matrix of the mixed model equation, as previously defined [17], can be used to calculate each PEV estimate in each individual. For each animal and trait, this study first calculated the standard error of prediction (or the square root of PEV), which was transformed into an estimate of the PEV. The only other element in the equation is the additive genetic variance or . Each trait was calculated individually using the restricted maximum likelihood (REML) method from the same dataset.
The genetic and phenotypic (co)variances were estimated using pairwise bivariate animal model implemented in MTG2 v2.22 software. The animal model for the analysis of two traits or bivariate analysis is written as [27]:
where, y1 and y2 represents the observation vectors corresponding to individuals for traits 1 and 2. The vectors b1 and b2 denotes the fixed effects for traits 1 and 2, while u1 and u2 are vectors representing the additive genetic effects for traits 1 and 2, respectively. The e1 and e2 are the vectors of residual effects for traits 1 and 2. X and Z are the incidence matrices related to effects b and u, respectively.
The genetic (rg), and phenotypic (rp) correlations were estimated using the following formula:
where , and are the genetic, and phenotypic covariance between traits X and Y; represents the additive genetic variance; is the phenotypic variance of the corresponding traits.
In addition, the coefficient of the genetic variation (CVg) was calculated as the square root of the additive genetic variance divided by the mean of the trait.
RESULTS AND DISCUSSION
Table 1 lists the summary statistics (mean, maximum, minimum, standard deviations, and phenotypic coefficient of variation) of the studied traits of 1,103 animals consisting of the Hanwoo population. The mean values for CI, AFC, GL, NAIPC, CWT, EMA, BF, and MS in this study were 378.43 days, 741.19 days, 286.45 days, 1.29, 374.86 kg, 87.81 cm2, 13.49 mm and 4.08, respectively. NAIPC (49.35%) showed the highest phenotypic variability. On the other hand, the phenotypic variability was lower in the GL among the reproductive traits and in the CWT among the carcass traits. The mean values for the reproductive traits are lower than those published earlier [28–32] and higher than in other studies [33,34]. Noticeable differences in the sample sizes among studies were found, which might explain some of the variations of estimation in the present study and other reports. A longer calving interval is often related to lower fertility due to an undesirable conception rate. A recent report [35] found that the average values for CWT, EMA, BF, and MS were 447 kg, 93.75 cm2, 12.80 mm, and 4.89, respectively, in the Hanwoo steer population. Another experiment on the Hanwoo population conducted over a period from 1989 to 2015 reported that the average for CWT, EMA, BF, and MS at approximately 24 months of slaughter age was 343.96 kg, 78.90 cm2, 8.71 mm, and 3.33, respectively [36].
A set of 41,445 common SNPs was selected after the QC test, which covered 79.52% of initial SNPs on all 29 Bos taurus autosomes (BTA). The markers were unsteadily distributed with substantial over-representation on certain chromosomes. BTA 1 contains the highest number of SNP markers (2,614), covering a length of 52.10 Mb, while BTA 28 had the lowest number of SNPs (714). Finally, Table 2 lists the SNP information after the IBS test and QC procedure.
The h2 and variance components were estimated with standard errors for all reproductive and carcass traits using the markers and phenotypic information, as presented in Table 3. The estimates of h2 for CI, AFC, GL, NAIPC, CWT, EMA, BF, and MS were 0.10 ± 0.05, 0.13 ± 0.05, 0.17 ± 0.06, 0.11 ± 0.04, 0.37 ± 0.07, 0.35 ± 0.07, 0.27 ± 0.06, and 0.45 ± 0.07, respectively. The average h2 values for the carcass and reproductive traits were estimated to be 0.13 and 0.36, respectively. Higher h2 values were observed in the GL among the reproductive traits and MS among the carcass traits. For the reproductive traits in this study, the estimated h2 values were in the range of low h2. The observed low h2 estimates were comparable to previously reported estimates in other beef breeds. Lopez et al. [34] reported low h2 estimates for a CI of 0.01, GL of 0.14 in Hanwoo cattle, and high h2 estimates for an AFC of 0.08 in the same breed. In Japanese Black (Wagyu) cattle, h2 estimates of 0.049 [31] and 0.047 [37] for CI, 0.215 [37], and 0.158 [31] for AFC, and 0.020 for NAIPC [31] were described. Yagüe et al. [32] reported estimated h2 of 0.085, 0.037, and 0.071 for CI, GL, and NAIPC, respectively. Several studies reported the estimates of heritability h2 for CI was 0.222 in Jersey × Red Sindhi [38], 0.105 [39], and 0.02 [40] in Nelore cattle, and 0.09 in Brahman-Angus cattle [41]. Alejandro et al. [42] reported a higher h2 of 0.20 for AFC in Simmental cattle.
h2, heritability; , genetic variance; , residual variance; , phenotypic variance; CVg, coefficient of genetic variance; CI, calving interval; AFC, age at first calving; GL, gestation length; NAIPC, number of artificial inseminations per conception; CWT, carcass weight; EMA, eye muscle area; BF, backfat thickness; MS, marbling score.
The h2 estimates for carcass traits in this study differ considerably from those obtained in previous studies by Naserkheil et al. [43]. They reported the h2 values for CWT, EMA, BF, and MS of 0.28, 0.46, 0.57, and 0.59, respectively, using the pedigree-based GBLUP method. Another report on the genetic analysis of carcass traits for Hanwoo beef cattle on 6,092 animals from 2005 to 2017 showed corresponding h2 values of CWT as 0.35±0.04, 0.43±0.05, 0.48±0.05, and 0.56±0.05, respectively, using a pedigree-based GBLUP model [35].
h2 estimates based on the 50K SNP Chip for CWT, EMA, BF, and MS in this present study agreed with those observed by Srivastava et al. [44] for a population of 7,324 Korean Hanwoo cattle. On the other hand, Lopez et al. [45] suggested that the estimated h2 with 50K SNP panel in Korean Hanwoo cattle for carcass traits was medium to high, ranging from 0.32 to 0.40 based on GRM.
According to CVg, the results showed significant additive genetic variation for NAIPC (15.50%), BF (22.34), and MS (31.58%), compared to relatively lower additive genetic variation for the other traits (0.96% to 8.59%). The evolvability of a trait is determined by its genetic variability [46], which impacts how easily traits can be altered by breeding. In other words, the predicted genetic gain for NAIPC, BF, and MS will be higher than other traits (using the standardized scale).
The low h2 estimate observed in our study can be attributed to several factors that warrant further discussion. Firstly, it is important to highlight that in our study, the h2 was calculated using markers and phenotypic information without access to pedigree records. The absence of pedigree information can impact the accuracy of h2 estimates, as pedigree records play a crucial role in capturing true genetic relationships among individuals. Studies that utilized pedigree information or a complete dataset of individuals have reported higher h2 estimates for carcass traits. Moreover, our study was limited by a relatively small sample size, and this factor can also influence the estimation of h2. A reduced sample size may result in diminished statistical power to accurately detect genetic effects. Given these limitations, it is expected that the h2 estimates for carcass traits in our study would be lower compared to investigations with pedigree information and larger sample sizes. Furthermore, there may be differences in the slaughter age of the animals, such as the number of records, the breed, differences in the fixed effects, and the statistical models used for analyses, which could account for the disparity between the estimates of this study and those of previous studies. In addition, the differences in h2 can be explained by the varying genotype-environment interactions. However, despite these challenges, our study provides valuable insights into the h2 of carcass traits using marker-based methods and highlights the need for more comprehensive studies with larger sample sizes and pedigree information to obtain more accurate h2 estimates.
The GEBV accuracy for reproductive and carcass traits in Hanwoo cows was estimated using the GBLUP and WGBLUP models with a complete data set. Generally, the predictive accuracy for most traits slightly varied between GBLUP and WGBLUP models (Table 4). The accuracy of the genomic predictions ranged from 0.51 to 0.60 in reproductive traits and 0.68 to 0.74 in carcass traits using the GBLUP model, whereas the accuracy ranged between 0.51 and 0.66 in the reproductive traits, and 0.72 and 0.79 in the carcass traits in WGBLUP model, respectively. The average accuracy for reproductive traits in the studied population was approximately 0.54 (GBLUP) – 0.57 (WGBLUP) and approximately 0.71 (GBLUP) – 0.76 (WGBLUP) for carcass traits. The average GEBV accuracy in the WGBLUP indicated more positive changes than GBLUP (5.6% in the reproductive traits and 6.7% in the carcass traits) among the GEBV estimates of all studied traits. In this study, the WGBLUP showed obvious superiority over the GBLUP method. Currently, the genomic selection is applied in beef cattle on a large scale, focusing mainly on the carcass traits [20,47].
Some studies have been conducted to evaluate the average prediction accuracy of genomic evaluations using GBLUP and ssGBLUP methods for the reproductive traits on different populations, such as Canadian Holstein [48] and Nelore cattle [49]. The genomic evaluation accuracy for the reproductive traits varied among breeds, the genetic architecture of the traits studied, statistical method, effects of SNPs, and the used SNP set. For AFC, Laodim et al. [50] reported that the accuracy performance of the ssGBLUP model was 0.297 and between 0.23 and 0.33 for Thai crossbreed animals and Nelore cattle, respectively, using another three different Bayesian statistical methods [51] and appeared to be a lower value compared to the present findings.
In Nelore cattle, the average prediction accuracy ranged between 0.38 and 0.42 by GBLUP and Bayesian method for the same trait [52], which partially supports our results for AFC accuracy. Boddhireddy et al. [53] showed a higher accuracy of prediction in Nelore cattle using the BayesC method for reproductive traits, which was 0.64.
Some studies reported the performance of genomic prediction models for various traits in different breeds [54–56]. Kim et al. [58] observed high prediction accuracy using 919 Hanwoo cattle by the GBLUP method, and the prediction accuracies obtained for CWT, EMA, BF, and MS were 0.779, 0.758, 0.766, and 0.791, respectively. On the other hand, the genomic prediction accuracy varied among traits while using GRM constructed on a 50K SNP panel; the genomic prediction accuracy for CWT, EMA, BF, and MS were 0.63, 0.58, 0.55, and 0.56, respectively [45]. By contrast, lower accuracy was also observed using a 50K SNP chip for Korean Hanwoo cattle in the GBLUP method, with EMA, BF, and MS values ranging from 0.27 to 0.30, respectively [1].
Table 5 lists the genetic and phenotypic correlations among the reproductive and carcass traits. The genetic and phenotypic correlations between traits were analyzed using the genetic and phenotypic variance and the covariance of the two traits. The estimates of the genetic correlation between reproductive and carcass traits were low to high, ranging from −0.56 ± 0.03 to 0.61 ± 0.03. Acccording to Dahliani et al. [59], the correlation values were divided into the following categories: very low (0.00 to 0.19), low (0.20 to 0.39), moderate (0.40 to 0.59), strong (0.60 to 0.79), and very strong (0.80 to 1.00). Strong positive genetic correlations were found between GL and NAIPC (0.61 ± 0.03) and CWT and EMA (0.60 ± 0.02), as represented in Table 5, which were the highest correlations among the trait pairs. Furthermore, the strength of the associations between NAIPC and CWT (0.49 ± 0.03) and AFC and CWT (0.48 ± 0.03) were moderate and positive. Hence, the selection of these traits could be advantageous. This strong positive genetic correlation could be due to pleiotropy, wherein a gene or a set of genes influences two traits and results in the genetic correlation between these traits [60].
Positive phenotypic (0.05 ± 0.02) and genetic correlations (0.26 ± 0.0١) were observed between CI and AFC. The genetic associations between CI and AFC were stronger than the phenotypic correlations. Shin et al. [61] reported a comparable positive association between these traits in Hanwoo cows, which strongly supports the present study. The moderate genetic associations between reproductive traits have the same sign as patterns that can be observed phenotypically [62,63]. Gutiérrez et al. [64] reported a favorable genetic correlation (0.233) in beef cattle between CI and AFC. In contrast to the genetic association, which was only weakly positive (0.10), Lôbo [65] discovered a high positive phenotypic correlation between AFC and CI (0.43). In these results, AFC appears to be an important characteristic reflecting the reproductive health of cows. An improvement in the CI performance would result from the selection for a shorter AFC. Berry and Evans [66] estimated a positive genetic association of 0.22, while Lopez et al. [34] reported a correlation of 0.52; however, the genetic correlation between AFC and CI was only found to be between 0.09 [28] and −0.25 during the first 42 days of the calving season. In contrast, CI with AFC was a low negative correlation, which is not an agreement reported elsewhere [67,68]. They reported negative correlations between CI and AFC of −0.13 for Brahman cattle and −0.06 for Nelore cattle.
The calculated weak positive associations between GL and CI also agree with Lopez et al. [34]. The phenotypic correlation of 0.04 between GL and AFC is consistent with earlier investigations [34]. These outcomes resembled those in Nellore cows, as reported by Ulhôa Magnabosco et al. [69]. Oyama et al. [70] also mentioned the genetic relationships between GL and CI of 0.16. Bekele et al. [71] reported strong positive genetic correlations between GL and CI in Fogera cattle, 0.72.
The strongest correlation among all the trait pairs in this analysis was obtained between GL and NAIPC (0.61 ± 0.03), which showed a significant genetic relationship. On the other hand, the CI showed the highest negative correlation with NAIPC (−0.56 ± 0.03) and AFC with GL (−0.41 ± 0.02). Similar findings have been achieved in Japanese Black cattle by Setiaji and Oikawa [72], who reported the positive genetic and phenotypic correlation between NAIPC and GL. NAIPC was recorded before conception, and GL represents a heifer’s ability to sustain the pregnancy until the day of calving. As a result, the strong genetic link shows that these two traits are related genetically and might be influenced by a group of genes. As a result, choosing one of the traits would have a significant impact on the other.
This study found that estimates of genetic association between traits ranged widely. The traits of Hanwoo cows, CWT and EMA, are highly and positively associated, suggesting that animals with a higher EMA will result from selection for increasing the CWT. This correlation estimate was similar to that of Park et al. [73] and Choi et al. [74], who used Hanwoo males to report values between 0.52 ± 0.08 and 0.55 using similar features. Other Hanwoo research revealed the same positive association [35,43,75–77]. The association between CWT and EMA was supported by several different studies involving Angus [78–81], Brangus [82,83], Angus–Brahman [84], Canadian crossbred cattle [85], Nellore cattle [86], Heriford, Simmental [87], Brazilian Nelore [88], Brahman [89,90], and other crossbred cattle [91].
The genetic correlation of BF with CWT (−0.12 ± 0.03) and EMA (−0.18 ± 0.03) was negative, which is financially feasible for the beef industry because CWT and EMA will increase if BF decreases and make the carcass profitable. Davoli et al. [92] obtained similar results in Large White pigs and revealed negative genetic correlations between CWT and BF. In the case of the fat content, BF is associated with MS (0.35 ± 0.02), which increases the juiciness of the meat.
According to these findings, the genetic correlation between EMA and MS was determined to be positive and fairly moderate (0.28 ± 0.03), similar to the results from other research [74,89,90,93], but significantly lower than the estimate of 0.65 published by Hwang et al. [94] in Hanwoo population.
In this study, the findings of the genetic correlation between reproductive and carcass traits were moderate to low, or negative. All reproductive traits have moderate to weak positive genetic correlations with CWT. MacNeil et al. [95] also reported a lower correlation of GL with CWT, which was also close to zero. On the other hand, EMA showed positive genetic correlations between AFC (0.24 ± 0.03) and NAIPC (0.35 ± 0.03). Furthermore, BF also showed a weakly positive genetic correlation with CI and AFC. The highest positive genetic correlations between the reproductive and carcass traits were between NAIPC and CWT (0.49 ± 0.03) and AFC and CWT (0.48 ± 0.03). In contrast, negative genetic correlations were found between AFC and MS. Negative results have also been reported [96,97], showing that the AFC can be lowered by increasing the meat and fat deposition. Higher subcutaneous fat deposition may signal faster maturation and make animals more sexually precocious, but more research is needed. A lower fat content is better for reproduction in cows.
These studies showed that the strong phenotypic correlation of 0.66 ± 0.02 between CWT and EMA, which was the strongest correlation among all pairs of reproductive and carcass traits, followed by the weak positive correlations between EMA and MS, AFC, and NAIPC, between CWT and BF, and between CWT and MS which were 0.33, 0.30, 0.29, and 0.29, respectively. In the present study, the phenotypic correlation was within the range of estimates made previously for Korean Hanwoo [93], Angus [78,79], Brangus [82,83], Angus-Brahman [84], Canadian crossbred cattle [85], and Nellore cattle [86].
This study found low to moderate genetic correlations between the attribute of reproductive and carcass weight CWT, which may explain why choosing a heavier body weight may result in longer CI, AFC, GL, and increased NAIPC. The genotype-environment interaction is a more likely cause of the phenotypic manifestation of these traits because of the near-zero phenotypic association and the marginally favorable genetic correlation between CWT, AFC, and NAIPC. After producing a reference population for carcass and reproductive traits, the application of genomic selection would be preferable to address the limitations of this study. These findings on variance components, heritability h2 estimates, GEBV accuracy, and correlation coefficients for reproductive and carcass traits offer important insights into the genetic merits of Hanwoo cows. They may benefit future research on them and their incorporation into the Hanwoo National Evaluation for genomic selection.
















