INTRODUCTION
Research has indicated environmental influences such as temperature, precipitation, and soil physical and chemical characteristics on alfalfa (Medicago sativa L.) biomass production [1-5]. Kim et al. [6] were able to develop an alfalfa yield prediction model with climate and soil variables. Although the variables could explain the alfalfa yield variance at a marginal level, soil texture and growing degree days (GDD) were the most critical among the tested variables to explain the yield variance at around 63% and 32%, respectively. In an attempt to interpret delayed fall harvest’s impacts on alfalfa productivity in the following year, the accumulations of carbohydrates and amino acids in the alfalfa root system were evaluated at several fall GDD levels [7]. The research was able to propose a late fall harvest window based on GDD. When developing alfalfa production models, researchers consider the impacts of weather and soil conditions at the same time. Shroyer et al. [8], Park et al. [9], Shewmaker et al. [10], and John et al. [11] confirmed the effectiveness of precipitation, soil pH, and drainage class as the significant environmental factors affecting alfalfa production.
Some specific weather conditions, such as winter temperatures, are meaningful information to predict first-cut alfalfa yields in Michigan, USA [4]. The research valued the potential of the winter weather-related alfalfa yield prediction model as a management development tool. The performance of the alfalfa growth prediction model varies depending on the target component variables. The prediction models for alfalfa biomass production and crude fiber contents were reported to be more accurate than crude protein content [5].
Kim et al. [6] proposed a possible overestimation of weather influences on forage biomass because of the mutual relationships between the weather variables, as shown in sunshine duration and rainfall variables. Sunshine duration positively influences the phyllosphere bacterial diversity and community structure of the alfalfa field, along with soil temperature [7]. The soil moisture is mainly balanced by evaporation and rainfall; those variables must be involved in enhancing alfalfa productivity. Furthermore, these beneficial effects should be validated based on more research data.
Evaluation of alfalfa growing condition variables, for instance, some accumulated temperature and GDD estimated at ranges of aerial temperatures, had a chance of being eliminated in stepwise regressions even though the variables are some agricultural values. Therefore, consideration for preventing removals of associated weather variables will be necessary to maintain those kinds of variables in alfalfa prediction models.
Considering soil’s physical conditions as growing condition variables is challenging even though research adopted soil variables to interpret alfalfa yield variance [12]. Generally, soil physical properties are nominal or categorical data. For example, soil textures are categorized by the combinations of three different soil particle size groups; therefore, the soil texture data provided by the Korean Soil Information System (KSIS, http://soil.rda.go.kr) are discrete variables and cannot be analyzed by a general linear model approach. Furthermore, these physical characteristics may cause an overestimation of the soil impacts on alfalfa biomass due to possible overlapping of the texture effects. Therefore, data transformation is required to convert nominal soil variables into continuous values [13].
Annually, South Korea imports more than 220 kilotons of alfalfa hay from the USA by paying an approximately similar amount as the logistics costs. Also, the demand for high-quality alfalfa hay is steadily growing in neighboring countries such as Japan and China, which challenges securing the necessary alfalfa hay for the country’s dairy industry. Therefore, enhancing the production capacity of domestically produced alfalfa is required to achieve a more sustainable livestock industry. This study assessed alfalfa production potential using specifically coined weather and soil property variables.
MATERIALS AND METHODS
A total of 197 alfalfa field trial data were acquired from the database of the National Agricultural Cooperative Federation or Rural Development Administration of South Korea between 1983 and 2008 after eliminating some field trial data having missing information. The field trial data covers sites between 35° 00’ 58” N, 126° 42’ 39” E and 37° 22’ 15” N, 128° 23’ 25” E in central and southern regions. The meteorological information corresponding to each trial location, including daily temperature, precipitation, and sunshine duration, was collected from the Korean Meteorological Administration (KMA, Weather data service available at MET data portal, http://data.kma.go.kr). Along with the weather data, soil physical information, such as soil texture, drainage class, and slope, was acquired from the Rural Development Administration (RDA, Soil database; available at Korean Soil Information System, http://soil.rda.go.kr) of South Korea. After collecting the related data, the data file was arranged by year, location, planting date, harvest date, forage biomass, and corresponding weather and soil data.
Twenty-three environmental variables potentially affecting alfalfa biomass productivity were developed in accumulated temperatures, sunshine duration, daily temperature higher than 25°C January temperature, precipitation, and soil property.
Accumulated temperatures were calculated using several different base temperatures [14,15] at daily temperature ranges.
The Thigh, Tlow, and Tbase are daily high, daily low, and base temperatures, respectively. The daily mean temperatures 0°C–25°C, 0°C–30°C, and higher than were accumulated using 0°C as a base temperature. The base temperature 5°C was also applied for daily mean temperatures 5°C–25°C, 5°C–30°C, and above 5°C. Another base temperature of 10°C was applied for the ranges of 10°C–25°C, 10°C–30°C, and above 10°C.
Sunshine duration was counted by the hour or day within daily temperatures between 0°C and 25°C, or 5°C and 25°C. Since optimum alfalfa root and shoot growth were reported around 25°C [16,17], the two variables related to the daily temperature higher than 25°C were added to the model in the form of duration day and accumulated temperature. The temperature causing daily temperature higher than 25°C was calculated by adopting 25°C as a base temperature [1,8,18]. For the evaluation of winter temperature impact, the daily mean and daily low temperatures of January were considered.
The precipitation variables were developed by counting the number of days or the total amount when precipitation was greater than 0 or 5 mm. The physical properties of soil were compiled using a categorical scale [19]. The 3 soil textural classes (sandy loam; 0%–20% of clay content, silt loam;0%–27% of clay content, loam; 7%–27% of clay content) were used among the total 12 classes. The clay content was considered as a representative soil texture. Based on the slope, the drainage was considered for six levels, from 1 (low) to 6 (high). Finally, the soil properties were transformed into quantitative data using jitter-transformation [20]: J = X ± runif (n, –a, +a).
The X and J are soil variables, respectively, before and after the transformation. The runif is a uniform density function to generate a random value for each category, n is the sample size, and ± a is the range of noise considering individual categories.
Variables demonstrating high correlations with forage biomass productivity were selected among the variable categories [21]. Due to multiple range applications and mutual associations, there is multicollinearity among the climate variables (e.g., accumulated temperature, growth period, precipitation, and sunshine duration). Therefore, the overlapping correlations of weather variables with alfalfa productivity were controlled by excluding the correlations in variable selections. Since there are also probabilities of eliminating some variables containing agricultural values due to the multicollinearity, those variables were included in the model regardless of whether the partial correlation coefficients or factor scores were not high enough to be selected [22].
The factor analysis was referred to assess the relationship between variables and alfalfa production as follows:
where X denotes the variables containing the selected climate and soil variables, F is the weather and soil property factors, L is a matrix of the loading scores, and δ is the residual effect. The forage productivity (Y) is modeled with β and ε for matrix coefficient and residual effects, respectively. Meanwhile, the R2 of the multiple regression model was used to assess the performance of the models explaining alfalfa productivity with the selected climate and soil variables. The relationship between the variables and the factors was quantified as a score using the varimax rotation of factor analysis [20]. The jitter-transformation was performed with soil properties using R 3.6.0 statistical analysis [23]. Finally, the partial correlation, factor, and multiple regression analysis were performed using SPSS 24.0 (IBM, Armonk, NY, USA).
RESULTS
The average rainfall distribution and aerial temperature from 1983 to 2008 are presented in Fig. 1.
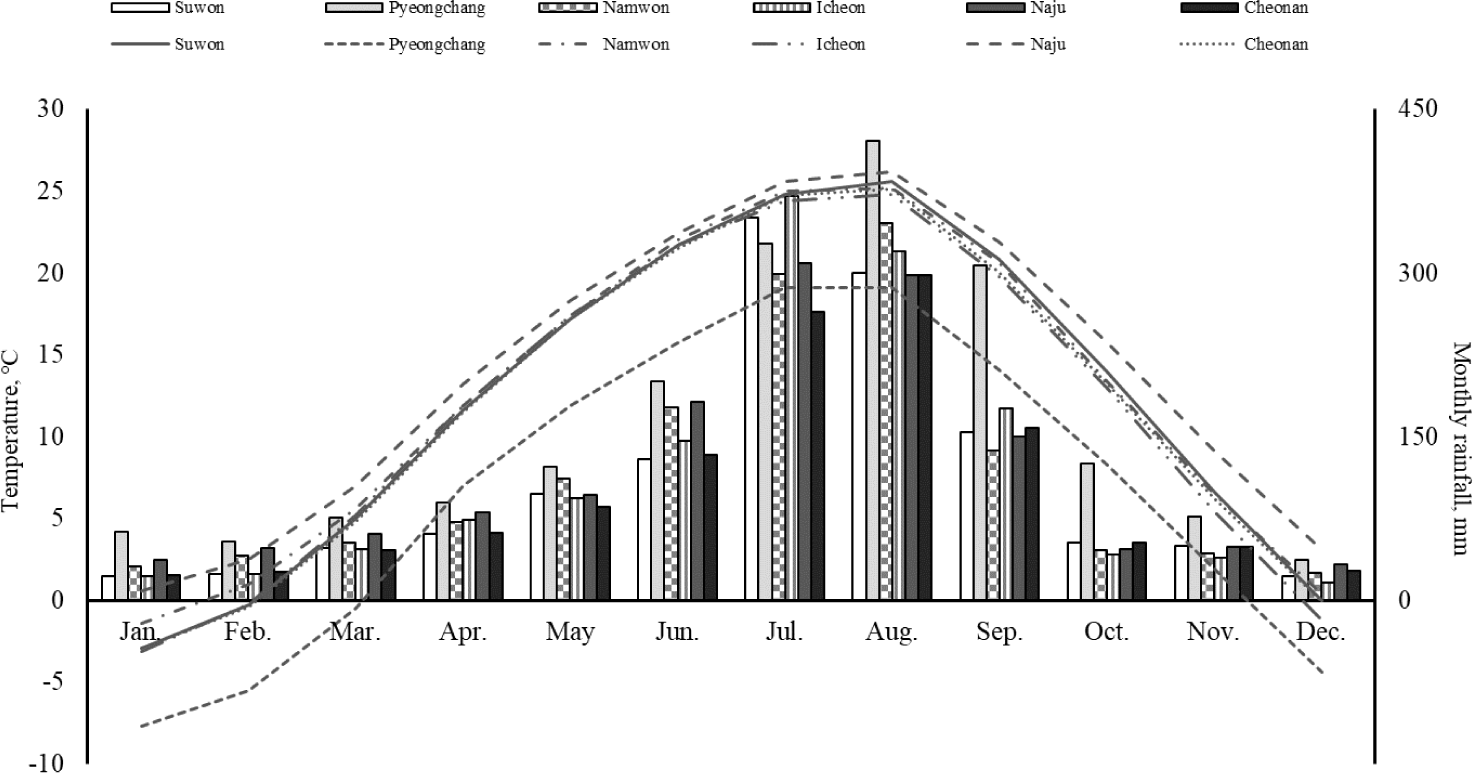
The rainfall demonstrated symmetrical distribution beginning from January to December. Rainfall is concentrated in the summer three months from June to August, which overlaps with the monsoon season in South Korea. Although monthly rainfall demonstrated a random pattern in the field trial locations, Pyeongchang (the eastern region) has more rainfall than other locations. After the monsoon, summer temperature frequently rises higher than 25°C in July and August at the field trial locations except for Pyeongchang. Winter begins in late December and lasts until March. The soil conditions corresponding to the field trial sites vary in the trial locations (Table 1).
| Mean | Minimum | Maximum | CV | |
|---|---|---|---|---|
| Before transformation | ||||
| Clay content (%) | 14.6 | 10.0 | 17.0 | 0.22 |
| Drainage (nominal) | 5.1 | 4.0 | 6.0 | 0.08 |
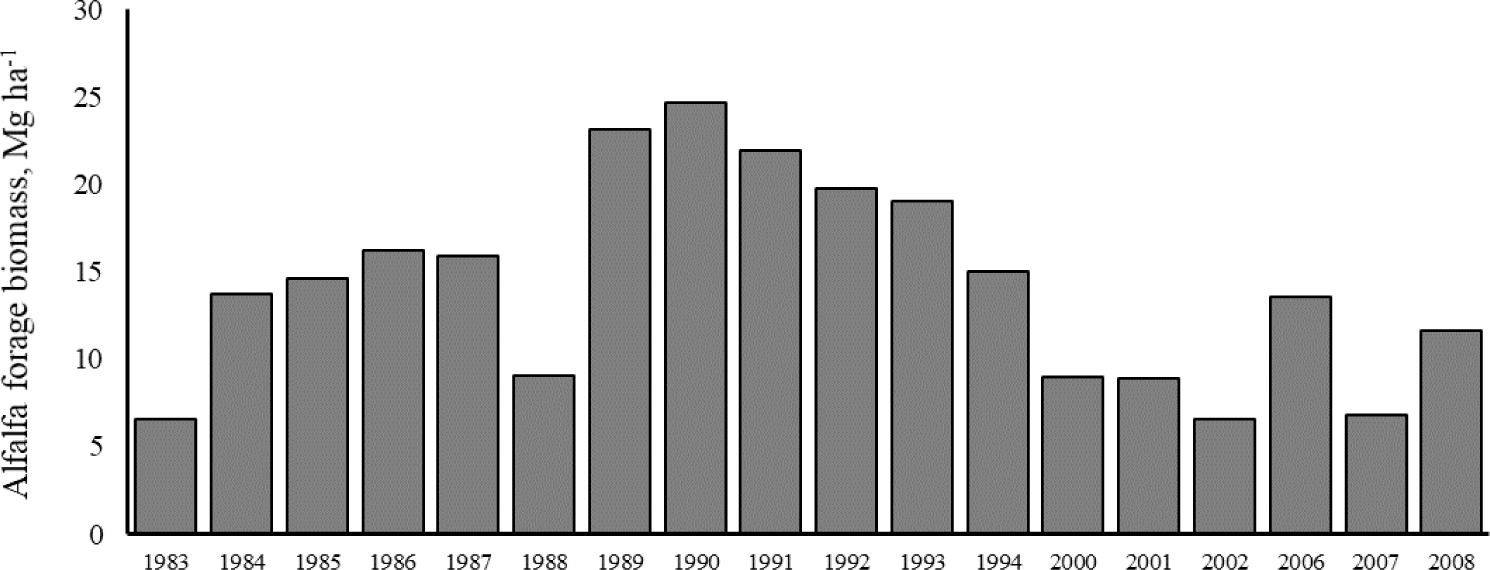
The mean alfalfa production was 13.7 Mg ha−1 and there were no significant trends in biomass production throughout the data collection years (Fig. 2). The means of alfalfa production obtained from the trial vary depending on the research purpose [24].
The variables assessed for estimating their impacts on alfalfa productivity were accumulated temperatures, sunshine duration, daily temperature higher than 25°C, January temperature, rain day, precipitation amount, and soil properties as presented in Table 2. The accumulated temperatures within the ranges of mean aerial daily temperature were approximately 1,000 to slightly over 5,000 when calculated at 5°C as a base temperature. The difference in the sunshine duration hours between the daily mean temperature ranges from 0°C to 25°C and 5°C to 25°C was approximately 339 hours. The daily temperature higher than 25°C was approximately two months long, and the accumulated temperature during this period was around 650°C. Contrasted to the daily temperature higher than 25°C, cold temperatures affect alfalfa’s winter survival. The January temperatures indicated subzero temperature even though the daily high was slightly above freezing temperature. The sum of rainy days averaged around 100 days. If the rain days were counted for more than 5 mm, the total rain day was reduced to half.
The amount of precipitation difference between over 0 and over 5 mm was about 120 mm. Since soil properties are nominal data, jitter-transformation was applied to make the variables continuous variables. However, the post-transformed soil properties, such as clay content and drainage, indicated substantial variations. In particular, the higher value of the jitter-transformed clay content indicated closer to sandy loam and loam than the lower value. Furthermore, the lower drainage value indicated less slope and drainage conditions.
The selection of growing condition variables potentially impacting alfalfa productivity is presented in Table 3. The two selection strategies were applied to the growing condition variable selections for factor analysis.
The selections were based on the high partial correlation coefficients with alfalfa productivity and also based on agricultural impact potential. The correlation coefficients of the growing condition variables, such as accumulated temperatures within the ranges of temperatures from 0°C to 25°C, 5°C to 25°C, and 10°C to 30°C were significant and highly correlated with alfalfa productivity (p < 0.01). The variable counted by hours for duration of sunshine between 5°C and 25°C was selected. The counting of days for the temperature duration between 0°C and 25°C was also selected (p < 0.05). The daily temperature higher than 25°C was counted by total days or accumulated temperature (p < 0.01). Although the low winter temperature variables in January by daily mean or by daily low were significant (p < 0.01), the daily low temperature variable was selected because of the slightly higher correlation coefficient. Rain day counted for over 0-mm was selected due to the significance (p < 0.05), even though the coefficient was not as high as the other variables. Although not statistically significant, the accumulated rainfall variable counted for greater than 0-mm precipitation was also intentionally considered in the assessment model. The partial correlation coefficient of the clay content in the field trial location soils was significant (p < 0.01), while drainage was not.
The impact of the selected growing conditions was summarized into dominant factors (spatial component) based on the eigenvalue of the scree plot (Fig. 3). The first three factors were selected.
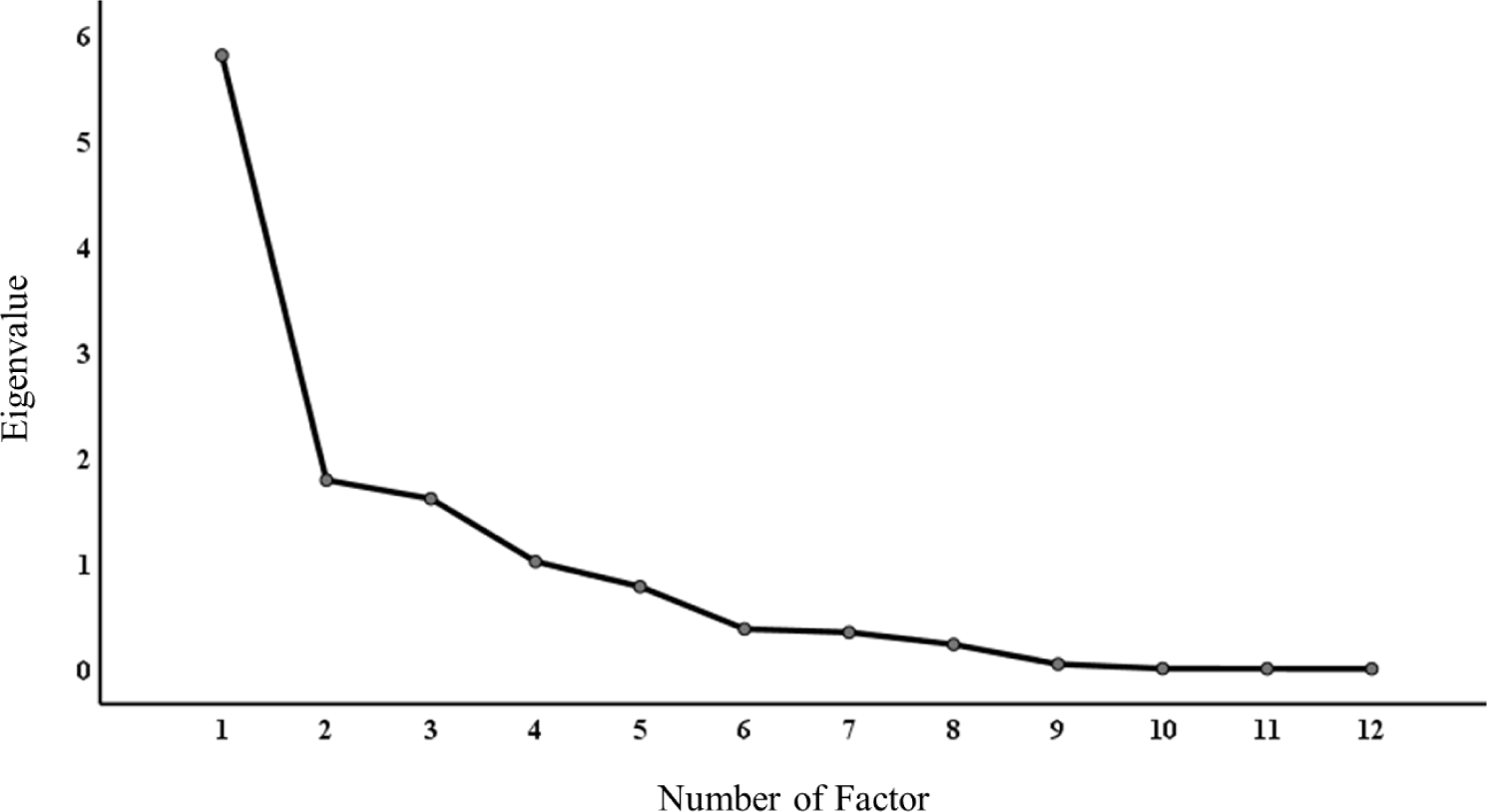
Table 4 indicated around 0.9 loading scores of the variables, such as accumulated temperature in the ranges of temperatures and daily temperature higher than 25°C in factor 1, while those of duration of temperature and January low-temperature variables were higher than any other selected growing condition variables in factor 2. In factor 3, the loading scores of the two precipitation variables were high. As shown in Table 5, the regression model’s three components were significant (p < 0.05). For the coefficient of determination (R2), Factor 1 could explain the variance of alfalfa production at 37.9%, which was improved up to 60.2% by including factors 2 and 3 in the regression model.
| Parameter | Standardized coefficient | p-value | VIF | R2 change | R 2 |
|---|---|---|---|---|---|
| Factor 1 | 0.633 | 0.000 | 1.002 | 0.379 | 0.602 |
| Factor 2 | 0.485 | 0.000 | 1.001 | 0.210 | |
| Factor 3 | 0.115 | 0.012 | 1.001 | 0.013 |
DISCUSSION
The impacts of weather and soil property variables on alfalfa productivity were assessed through a series of statistical analyses such as partial correlation, factor analysis, and stepwise multiple regression. In the growing condition variable selections, all the accumulated temperature variables demonstrated relatively high partial correlation coefficients with alfalfa productivity (Table 3). Since the inclusion of more than several growing condition variables within the same category may cause an overestimation of the correlation with the alfalfa productivity, three accumulated temperature variables were selected among them. Also, due to the substantial variations in yearly growing conditions and alfalfa production responses, some strategic analysis approach was necessary to keep the potentially meaningful growing condition variables. Although rainy day, accumulated rainfall, and clay content were not highly correlated to the alfalfa productivity, those variables were also included in the factor analysis to balance the evaluation of growing condition variables on alfalfa production.
In this study, the impacts of climate and soil property variables on alfalfa productivity were approximately 60.2%, where the three dominant factors were identified. The daily temperature higher than 25°C was most contributing to the alfalfa biomass along with the accumulated temperature variables in factor 1. The duration of sunshine at daily temperature at a range of 0°C–25°C and rainfall were most contribution in factor 2 and 3, respectively, which indicated those two variables are perpendicular to each other as anticipated. Factor 3 explained only 1.3% of the alfalfa production variance (Table 5). The actual data points of alfalfa forage biomass spread more from the biomass prediction line between 5 and 12 Mg DM ha–1 than the higher production levels, 15 Mg DM ha–1 (Fig. 2).
In this study, extreme aerial temperature conditions such as daily mean temperature higher than 25°C and winter January temperature were presumed to influence alfalfa biomass accumulation negatively. However, the evidence of the negative impacts could not be confirmed with the collected alfalfa data because of the insignificance of the partial correlation coefficients of those two extreme weather conditions. Although winter hardiness of alfalfa cultivars has been crucial in alfalfa cultivar selections in the USA [25], the partial correlations of the winter temperatures with the alfalfa productivity remained positive in this study, suggesting that the temperature did not behave as a critical factor for winter survival. Some information about winter survival in the USA indicated winter dormant varieties can survive at −15°C [18]. However, the monthly average is −5.5°C in January [26]; the daily low rarely drops to −15°C in South Korea. Therefore, winter survival should not be a major factor determining alfalfa production in the next growing season [6].
Another reason for the lack of the presumed negative impacts might be explainable by the alternating winter aerial temperature changes by 3- or 4-days intervals between the freezing and mild winter weather. Also, the presumed adverse effects of summer temperatures higher than 25°C could not be confirmed in the study. According to KMA [26], the daily mean temperatures from July to August were around 29°C. Therefore, stunts in alfalfa growths could occur in summer, as possibly noticed in cool-season grass. However, the positive partial correlation coefficient between daily temperatures higher than 25°C and biomass productivity indicated a lack of evidence for heat stress in South Korea. The temperature above the ideal cool season grass growth did not evidence any production reductions. Perhaps, the accumulated rainfall demonstrated a negative correlation, however, the values were low and insignificant (p = 0.78).
Alfalfa seems to start growing even below 5°C in Korean environment which is supported by a growth chamber study [25]. Therefore, it is necessary to study the alfalfa growth response in early spring in South Korea. Although 5°C has been frequently adopted as a base temperature in alfalfa GDD calculation [15], considering 0°C as a base temperature could be meaningful by extending the available growing season by 60 days longer than reported cool season grass [27]. The advantages of the greater GDD may be realized in improved alfalfa production capacity in South Korea [28].
Since alfalfa is a high-water demanding forage crop [29-31], the leading alfalfa exporting states on the west coast of the USA depend heavily on irrigation. Unlike those states, the amount of rainfall or soil moisture did not appear as a significant alfalfa production limiting factor. On the contrary, the high temperature and high humidity in conjunction with the strong wind in summer monsoon may be the more challenging growing conditions in South Korea. The current study did not assess the impact of seasonal growing conditions possibly affecting alfalfa production. Although the alfalfa productivity models have limited values as prediction tools due to weather data availability before a particular time, the quantified influences of the growing condition variables provided a substantial understanding of each variable’s influence on alfalfa production. These aspects can be further realized in planning alfalfa cultivar selection, harvest frequency, and seasonal utilization adjustment in the diverse regions of South Korea.
In this study, the impact of two variables on the daily temperature higher than 25°C was positive on alfalfa production. It implies that aerial temperature higher than 25°C did not negatively influence alfalfa growth, although 25°C was reported as optimum root and shoot growth for alfalfa [16]. The degree of heat stress differs by the available soil moisture, and the stress is hard to measure in the separation of drought stress. As reported [16,17,25], alfalfa can grow in various temperatures, such as from 0°C to 40°C, if irrigation is available. Since KMA [26] indicated the hottest summer months, July and August temperatures rarely rise above 35°C, alfalfa production loss due to heat stress must be rare in Korea. The distribution of rainfall is critical for enhanced biomass production [32]. However, the impact of rainfall was insignificant in this study (Table 4). As presented in an arid area that requires irrigation [33], available soil moisture balance is critical in alfalfa production rather than rainfall amount during the growing season.
CONCLUSION
Since the tested growing condition variables could explain the variance of alfalfa biomass production at around 60 %, the model performance is marginal as a prediction model. Probably, this level of the model performance can be reasoned from some heterogeneous characteristics of alfalfa field research settings and the lack of standardization of obtained data under the various study goals. However, this study could quantify the impacts of large numbers of weather and soil variables on alfalfa productivity through specifically coined weather and soil variables using statistical analysis approaches. Since this modeling effort is novel, adding more standardized alfalfa field trial data or considering seasonal aspects is required in future modeling works.
















